FUNZIONE DI HEAVISIDE, FUNZIONE UNIT STEP, FUNZIONE GENERALIZZATA DELTA DI DIRAC

 FUNZIONE DI HEAVISIDE

Si tratta di una funzione così definita:

É anche detta funzione tetha o funzione gradino.

Funzione di Heaviside.

FUNZIONE UNIT STEP 

Si tratta di una funzione così definita:



{\ displaystyle H [n] = {\ begin {cases} 0, & n <0, \\ 1, & n \ geq 0, \ end {casi}}}

Tale funzione presenta una discontinuità di prima specie in x = 0, in quanto:

lim  U(x)= 1 ; lim U(x) =0 

 x→ 0+              x → 0-

con salto di discontinuità pari a 1.

Funzione Unit Step.

LE FUNZIONI PRESENTATE HANNO IN COMUNE IL PUNTO DI DISCONTINUITÀ DI PRIMA SPECIE CON LA DIFFERENZA CHE LA HEAVISIDE NON É DEFINITA IN ZERO.

Identificazione della funzione di Heaviside con la Unit Step:

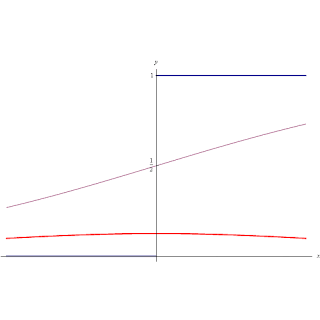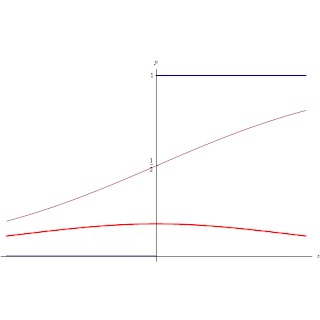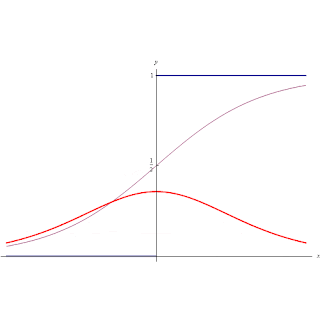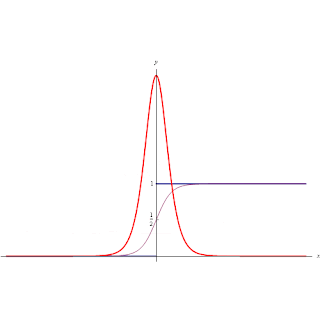Funzioni di Heaviside, Unit Step, Delta di Dirac.

La derivata prima della funzione Unit Step è la funzione generalizzata Delta di Dirac.
(funzione in rosso in animazione)

LA FUNZIONE UNIT STEP E LA DELTA DI DIRAC sono utilizzate per applicazioni in campo fisico per lo studio di segnali attivati in un dato istante e mantenuti costanti successivamente.
La funzione generalizzata Delta di Dirac è, infatti, anche detta funzione impulsiva.

{\displaystyle \Theta (x)={\begin{cases}0,&x<0\\1,&x\geqslant 0\end{cases}}}

SISTEMI DI COORDINATE.

SISTEMI DI COORDINATE:

È importante scegliere il sistema più appropriato in relazione a come il moto (ad esempio di un punto materiale) è stato generato ed in relazione alla forma dei dati forniti. 

Fra i sistemi di coordinate possibili si distinguono le coordinate polari da cui si possono ricavare quelle cilindriche e sferiche come naturale espansione del sistema polare nelle tre dimensioni.

Passaggio da coordinate sferiche a coordinate cilindriche (3D)

COORDINATE POLARI

Sistema di coordinate polari (2D)

x= ρcos θ 

    y=  ρsin θ

                         Sistema di coordinate sferiche.

COORDINATE SFERICHE                                                        

x= ρ sin φ cos θ 
y=  ρ sin φ sin θ
z=  ρcos  φ 

                                            

                                               
COORDINATE CILINDRICHE

{\displaystyle {\begin{aligned}x&=\rho \,\cos \phi \\y&=\rho \ \sin \phi \\z&=z\end{aligned}}}                         

                       

 

Sistema di coordinate cilindriche.